البــــايزيون والتكـــــــراريون
Bayesians and frequentist
د خالد أحمد جلال
أستاذ علم النفس المساعد (المشارك)، آداب المنيا
في كثير من الأحيان يصنف الإحصائيون أنفسهم على أنهم إما تكراريين أو بايزيين ، والحق أن كلا المعسكرين غير منفصلين تماما. وكل من المدرستين تقدم أدلة حول اختبار الفروض، وعلى الرغم من شيوع مدرسة التكراريين (الإحصاء التقليدية) في البحوث والدراسات النفسية والتربوية، حيث استخدام القيم الاحتمالية (P. Values) وفترات الثقة والاهتمام بالاحتمالات حول إحصاء الاختبار الإحصائي وذلك لاختبار أن الفرض الصفري صحيح، ولكنها لا تحدد سلفا الاحتمالات النسبية المرتبطة بكل من الفرض الصفري والفرض البديل، بينما البايزيون يستخدمون الاحتمالات القبلية apriori والتي تحدد بطريقة ذاتية، ويصلون منها إلى الاحتمالات البعدية posteriori.
في الاحتمالات، أعظم شيء في تحليل بايز أنه يخبرنا بما نريد أن نعرفه حقا، ألا وهو: احتمالية أن الفرض الصفري صحيح، دعنا نتعرف على عظمة تحليل بايز ونوضح كيف يعمل؟
مثال: بفرض أنه يوجد مرض ما وأن لهذا المرض وجود في المجتمع (انتشار)، وأن هذا المرض لا توجد له أعراض واضحة في مراحله المبكرة، تم عمل فحص تشخيصي لهذا المرض، ونحن نعرف أن هذه الفحص يعطي إجابة صحيحة بنسبة 99% ، تم اختيار فرد ما من المجتمع وقد أظهرت نتيجة الفحص أنه مصاب بالمرض، فما احتمالية أنه مصاب حقا؟
وبسؤل الفرد عن مرضه يجيب أنه متأكد بنسبة 99% من أنه مصاب، وإذا فكرنا أن هذا التشخيص غير صحيح، فإننا هنا نختبر الفرض الصفري من أن هذا الفرد غير مصاب بالمرض، وهذه النتيجة تخبرنا ذلك باحتمال 1%، ولكن هذه ليست احتمالية أن الفرض الصفري صحيح، وإنما الفرد مصاب بشرط أن الفرض الصفري الذي ينص على أنه غير مصاب أي P(D ǀ H0)
نحن نحتاج أن نعرف احتمالية أن هذا الفرد غير مصاب حقا بالمرض، ونريد أن نعرف معلومة أخرى إضافية قبل أن نعمل على ذلك ألا وهي الاحتمال الأولي Prior probability هذا الاحتمال الأولي هو أن الفرض الصفري صحيح، وذلك قبل أن نختبر إصابة الفرد بالمرض، بمعنى آخر نسبة الأفراد المصابون بهذا المرض في المجتمع، دعنا نقول أن هذه النسبة هي 1%، هنا توجد طريقتان للعمل على هذه الاحتمالية من أن الفرد لديه المرض حقا:
الطريقة الأولى:
نعلم أن تنظير بايز مشتق من قاعدة الضرب في الاحتمال الشرطي والذي ينص:
P (A ǀ B) = P (AՈB) / P (B) ----------- (1) P (B) ≠ Zero
وبضرب الطرفين في الوسطين ينتج:
P (AՈB) =P (A ǀ B) X P (B) ----------- (2)
وبدخول حدث تعسفي (D) Exhaustive وهو التشخيص فإنه يتقاطع مع الاحتمالين للفرض الصفري H0 والفرض البديل H1بأن الشخص مصاب بالمرض تنتج قاعدة بايز: (باستبدال الحدثين A و B بـ D و H0 ).
P (H0 ǀ D) = P(D ǀ H0) X P(H0) / P(D ǀ H0) X P(H0) + P(D ǀ H1) X P(H1) ------ (3)
حيث:
P(D ǀ H0) = 0.01 وهي احتمالية الحصول على نتيجة إيجابية بشرط أن الفرض الصفري صحيح.
P(D ǀ H1) = 0.99 وهي احتمالية الحصول على نتيجة إيجابية بشرط أن الفرض البديل (الفرد مصاب بالمرض) صحيح.
P(H0) = 0.99 الاحتمالي الأولي للفرض الصفري بأن الفرد ليس مصابا بالمرض.
P(H1) = 0.01 الاحتمال الأولي للفرض البديل بأن الفرد مصابا بالمرض.
وبالتعويض في معادلة (3) السابقة:
P (H0 ǀ D) = 0.01 x 0.99 / 0.01 x 0.99 + 0.99 x0.01 = 0.0099 / 0.0099 + 0.0099
= 0.0099 / 0.0198 = 0.5
وهذا يعني أنه إذا كان التشخيص يشير إلى أن الفرد بنسبة 99% مصاب بالمرض، فإن ذلك يعني أنه يوجد احتمال 50% أن يكون الفرد مصاب فعليا بالمرض.
الطريقة الثانية:
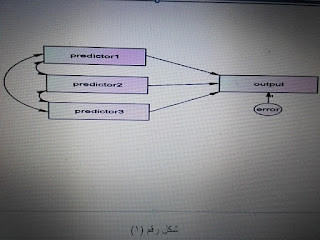
شكل (1) يبين بالمثال تحليل بايز
وهي طريقة طويلة لكن سهلة الفهم، من شكل (1) السابق، بفرض أن لدينا مجتمع حجمه 10000 شخص، وتم إجراء اختبار تشخيصي لهم، وبفرض أن احتمالية الإصابة بالمرض هي 1% ، من ثم نتوقع أنه من بين الـ 10000 فرد يوجد 100 فرد لديهم المرض والباقي 9900 ليس لديهم المرض، ونحن نعلم أن التشخيص يكون صحيحا للمرض بنسبة 99% ، لذا فإن من بين 100 فرد سنجد أن 99 فردا منهم يتم تشخيصهم إيجابيا.
أما الـ 9900 المتبقين الذين ليس لديهم المرض فإننا نعرف أن التشخيص يعطي نتيجة إيجابية بنسبة 1% ومن بين هذا العدد نتوقع أن 99 فردا مصابون بالمرض (تشخيص إيجابي).
من هنا لدينا 99 فردا غيرمصابين بالمرض ولهم تشخيص إيجابي، و 99 فردا ليس لديهم المرض ولهم تشخيص إيجابي، ومن ثم تكون النتيجة 99 + 99 = 198 فردا لديهم تشخيص إيجابي نصفهم ليس لديهم المرض. أي بنسبة 50% (وهي نفس النتيجة التي توصلنا إليها في الطريقة الأولى).
مما سبق يتبين لنا عظمة تحليل بايز في أنه يخبرنا بما نريد أن نعرفه حقا وهو احتمالية الفرض الصفري، وهذا أفضل بكثير مما تخبرنا به الدلالة الإحصائية أو (P. Value).
- Miles J. and Banyard Ph. (2007). Understanding and Using Statistics in Psychology a Practical Introduction or, how I came to know and love the standard error. London, SAGE Publications. (Pp. 315-319).
تعليقات
إرسال تعليق